California requires the Average or the Geometric Mean to be reported as a Median if any values in the data set contains a data qualifier (i.e. <,ND, DNQ, etc...). WIMS Spread Functions GAVGMEDZ, GGMMEDZ, and STATZ support these calculations.
The following is the Rule as stated in a typical California Permit:
When determining compliance with an average monthly limit and more than one sample result is available in a month, the discharger shall compute the arithmetic mean unless the data set contains one or more reported determinations of detected but not quantified (DNQ) or not detected (ND). In those cases, the discharger shall compute the median in place of the arithmetic mean in accordance with the following procedure:
(1) The data set shall be ranked from low to high, reported ND determinations lowest, DNQ determinations next, followed by quantified values (if any). The order of the individual ND or DNQ determinations is unimportant.
(2) The median value of the data set shall be determined. If the data set has an odd number of data points, then the median is the middle value. If the data set has an even number of data points, then the median is the average of the two values around the middle unless one or both of the points are ND or DNQ, in which case the median value shall be the lower of the two data points where DNQ is lower than a value and ND is lower than DNQ. If a sample result, or the arithmetic mean or median of multiple sample results, is below the reported ML, and there is evidence that the priority pollutant is present in the effluent above an effluent limitation and the discharger conducts a pollutant minimization program (PMP)16 (as described in Section I.7.), the discharger shall not be deemed out of compliance.
Other permits state: (which implies Geometric Mean should also be calculated as a Median if data qualifiers exist)
When determining compliance with a measure of central tendency (arithmetic mean, geometric mean, median, etc...) of multiple sample analyses and the data set contains one or more reported determinations of detected but not quantified (DNQ) or not detected (ND), the Permittee shall compute the median in place of the arithmetic mean in accordance with the following procedure:
1. The data set shall be ranked from low to high, ranking the ND determinations lowest, DNQ determinations next, followed by quantified values (if any). The order of the individual ND or DNQ determinations is unimportant.
(2) The median value of the data set shall be determined. If the data set has an odd number of data points, then the median is the middle value. If the data set has an even number of data points, then the median is the average of the two values around the middle unless one or both of the points are ND or DNQ, in which case the median value shall be the lower of the two data points where DNQ is lower than a value and ND is lower than DNQ.
You can use the STATZ, GAVGMEDZ function to calculate your Average Median. The following examples use the STATZ function to calculate the "AVG_MED" and "AVG":
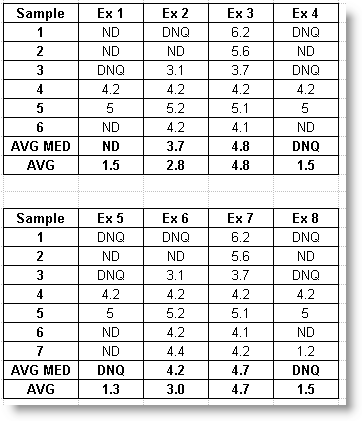
Example 1: Since the values contain a DNQ and an ND, we take the Median. Therefore sort the 6 values (ND, ND, ND, DNQ, 4.2, 5), take the 2 middle numbers (ND, DNQ) since there is an even number of values and take the lower of the 2 values - ND.
Example 2: Since the values contain a DNQ and/or an ND, we take the Median. Therefore sort the 6 values (ND, DNQ, 3.1, 4.2, 4.2, 5.2), take the 2 middle numbers (3.1, 4.2) since there is an even number of values and take the average of those 2 numbers - 3.7.
Example 5: Since the values contain a DNQ and an ND, we take the Median. Therefore sort the 7 values (ND, ND, ND, DNQ, DNQ, 4.2, 5), take the middle number (DNQ in the 4th position) since there is an odd number of points - DNQ
Example 7: There are no DNQ or ND values, take the average of the values - 4.7
Use GGMMEDZ to calculate the Geometric Mean or Median.